Trigonometry: Angles and Arcs, Part 1

CLICK HERE to view the YouTube video that corresponds to this post.

Please note that all calculator keypad instructions are intended for TI-83 through TI-84 Plus Silver Edition graphing calculators. Refer to your instruction manual to find specific keys for any other calculator.

This is part one of two posts that deal with angles and arcs. In this segment, I will cover some definitions pertaining to angles, how to find complementary and supplementary angles to a given angle, finding coterminal angles to a given angle, and converting between DMS notation and decimal degrees.

To begin this discussion, let's review some definitions pertaining to angles.

A straight angle is an angle that measures 180 degrees. A right angle is an angle that measures 90 degrees. An acute angle is an angle that measures between 0 and 90 degrees. And an obtuse angle is an angle that measures between 90 and 180 degrees. A quadrantal angle is an angle which has a terminal side on an axis line. Non-quadrantal angles can be identified by their quadrant number.

Two positive angles are said to be complementary if their sum is equal to 90 degrees. And two positive angles are called supplementary if their sum is 180 degrees.

First, we will discuss how to find a complementary or supplementary angle to a given angle. If you are given an angle, subtract it from 90 degrees to find its complement and subtract it from 180 degrees to find its supplement. Below are a few examples.

An angle is coterminal to a given angle if it contains only the addition of an integer multiple of 360 degrees. For example, the angles 45 degrees and 1170 degrees are coterminal because 1170 = 45 + 360(2). You may be asked to find an angle that is coterminal to a given angle. You only need to follow these easy steps to answer a question like this.

How to Find a Coterminal Angle
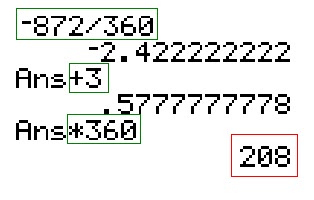
Step 1: Divide the given angle by 360 degrees. If the answer is positive, subtract whatever whole number you obtain from this. If the answer is negative, add subtract the whole number (including the sign!) minus 1. That is, if –n.kkk is the number, you will subtract (-n – 1) from the number. See example below for more clarification.
Step 2: Multiply this answer by 360 degrees to obtain the angle less than 360 degrees that is coterminal with the given angle. Two examples are below.

All of this can be accomplished very easily in your calculator. Input the given angle and divide by 360. If you then hit plus or minus, it will bring down the previous answer automatically. Here is how the screen looks.

The green, boxed items are what I manually typed into the calculator. Each "Ans" was automatically entered by the calculator when I hit the next operations key. The red boxed value would be my answer.

There are two ways to represent angle measures. The first is decimal degrees, as you probably are used to. These are angles such as 27.2 degrees or 108.3 degrees. Another way to represent angles is in DMS (Degrees, Minutes, and Seconds).

Just as there are 60 seconds in a minute when discussing time, there are 60 seconds in one minute when discussing angle measures. And, degrees work similar to hours in that there are 60 minutes in one degree. Therefore, there are 3600 seconds in one degree. These conversion factors will allow you to interconvert between these two angle representations. I will first show you how to do this manually, then will show you the "shortcut" by using your calculator's DMS conversion tool.

How to Convert FROM DMS TO Decimal Degrees
Step 1: Write the degrees, minutes, and seconds as a sum.
Step 2: Leave the degree term as is. Multiply the minutes term by the minutes-degrees conversion factor. Multiply the seconds term by the seconds-degrees conversion factor.
Step 3: Add.

How to Convert FROM Decimal Degrees TO DMS
Step 1: Split at the decimal point and write as whole degrees plus partial degrees.
Step 2: Multiply the partial degrees by the degrees-minutes conversion factor.
Step 3: If this is a whole number, then tack 0'' to the end of your answer. If it is a decimal answer, split it at the decimal point and write as whole minutes plus partial minutes.
Step 4: Multiply the partial minutes by the minutes-seconds conversion factor.
Step 5: Rewrite your answer without the plus signs.

It is important for you to know how to manually convert between decimal degrees and DMS, but your calculator provides a shortcut. Locate the ANGLE key on your calculator (this is the same as the APPS key which has different-colored lettering on it). To get into the ANGLE menu, hit 2ND, then APPS. In the ANGLE menu, you will find various items pertaining to angle measures. The ones we are interested right now are numbers 1 through 4. Number 1 allows you to enter the degree sign into your calculator; number 2 allows you to enter; number 3 allows you to enter radians into your calculator (to be dealt with in another post); and number 4 is what you use to instruct your calculator to convert into DMS form. To type the seconds symbol into your calculator, press ALPHA then the PLUS key.

First, make sure your calculator is in degree mode. To do so, press the MODE key (to the right of the 2ND key) and arrow down until you see RADIAN DEGREE. Ensure that DEGREE is highlighted black. If it is, press 2ND then MODE to return to the home screen. If it is not highlighted, arrow down to RADIAN, then arrow to the right to DEGREE, and then press ENTER. Press 2ND then MODE to exit the mode menu.

How to Use the Calculator to Convert TO DMS Form
Step 1: With your calculator in DEGREE MODE, type in the decimal degree form of the angle measure you wish to convert INTO DMS form.
Step 2: Open the ANGLE menu by pressing 2ND then APPS.
Step 3: In this menu, arrow down to option 4: >DMS and press ENTER (or simply press the number 4 on the keypad).
Step 4: Press ENTER to instruct the calculator to make the conversion for you. The angle measure in DMS will appear, rounded to the nearest whole second.

Here is what the calculator screen will look like.

How to Use the Calculator to Convert FROM DMS Form
Step 1: With your calculator in DEGREE MODE, input the angle measure in DMS form into the home screen. Type in the degree value, then open the ANGLE menu (2ND, APPS) and choose option 1: degrees. Then type in the minute value, open the ANGLE menu and choose option 2: minutes. Finally, type in the second value and press ALPHA (below the 2ND key) and then the PLUS key to input the seconds symbol.
Step 2: Press ENTER to return the angle measure in decimal degree form.
Here is what the calculator screen will look like. When reporting your answer, round according to the instructions given for your problem. If no rounding instructions are given, round to the hundredth (two decimal places) degree. (In the screen shot below, the reported answer would actually be 35.26 because the 5 would be rounded up.)

In part 2, we will look at radians and arc lengths.